Can you imagine that a number is equal to the sum of the cubes of its digits? Take the time to explain exactly what this means. This should begin to "set them up" for this most unusual phenomenon. By the way, this is true for only five numbers. Below are these five most unusual numbers.
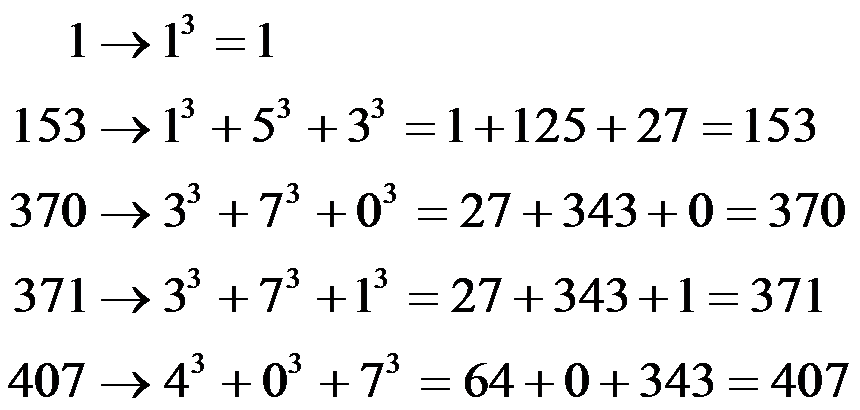
Students should take a moment to appreciate these spectacular results and take note that these are the only such numbers for which this is true.
Taking sums of the powers of the digits of a number leads to interesting results. We can extend this procedure to get a lovely (and not to mention, surprising) technique you can use to have students familiarize themselves with powers of numbers and at the same time try to get to a startling conclusion.
Have them select any number and then find the sum of the cubes of the digits, just as we did above. Of course, for any other number than those above, they will have reached a new number. They should then repeat this process with each succeeding sum until they get into a "loop." A loop can be easily recognized. When they reach a number that they already reached earlier, then they are in a loop. This will become clearer with an example.
Let's begin with the number 352 and find the sum of the cubes of the digits.
The sum of the cubes of the digits of 352 is: 33 + 53 + 23 = 27 + 125 + 8 = 160.
Now we use this sum, 160, and repeat the process:
The sum of the cubes of the digits of 160 is:
Again repeat the process with 217:
The sum of the cubes of the digits of 217 is: 23 + 13 + 73 = 8 + 1 + 343 = 352.
Surprise! This is the same number (352) we started with.
You might think it would have been easier to begin by taking squares. You are in for a surprise. Let's try this with the number 123.
Beginning with 123, the sum of the squares of the digits is: 12 + 22 + 32 = 1 + 4 + 9 = 14.
1. Now using 14, the sum of the squares of the digits is: 12 + 42 = 1 + 16 = 17.
2. Now using 17, the sum of the squares of the digits is: 12 + 72 = 1 + 49 = 50.
3. Now using 50, the sum of the squares of the digits is: 52 + 02 = 25.
4. Now using 25, the sum of the squares of the digits is: 22 + 52 = 4 + 25 = 29.
5. Now using 29, the sum of the squares of the digits is: 22 + 92 = 85.
6. Now using 85, the sum of the squares of the digits is: 82 + 52 = 64 + 25 = 89.
7. Now using 89, the sum of the squares of the digits is: 82 + 92 = 64 + 81 = 145.
8. Now using 145, the sum of the squares of the digits is: 12 + 42 + 52 = 1 + 16 + 25 = 42.
9. Now using 42, the sum of the squares of the digits is: 42 + 22 = 16 + 4 = 20.
10. Now using 20, the sum of the squares of the digits is: 22 + 02 = 4.
11. Now using 4, the sum of the squares of the digits is: 42 = 16.
12. Now using 16, the sum of the squares of the digits is: 12 + 62 = 1 + 36 = 37.
13. Now using 37, the sum of the squares of the digits is: 32 + 72 = 9 + 49 = 58.
14. Now using 58, the sum of the squares of the digits is: 52 + 82 = 25 + 64 = 89.
Notice that the sum, 89, that we just got in step 14 is the same as in step 6, and so a repetition will now begin after step 14. This indicates that we would continue in a loop.
Students may want to experiment with the sums of the powers of the digits of any number and see what interesting results it may lead to. They should be encouraged to look for patterns of loops, and perhaps determine the extent of a loop based on the nature of the original number.
In any case, this intriguing unit can be fun just as it is presented here or it can be a source for further investigation by interested students. We need to bring more of these "spectacular" math wonders to our students!
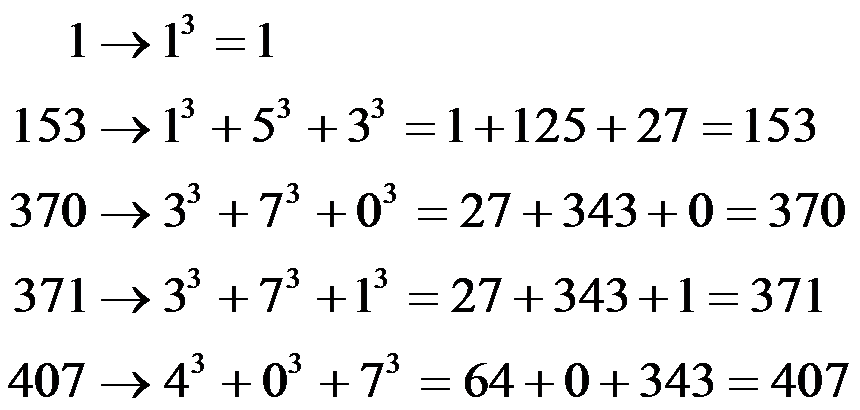
Students should take a moment to appreciate these spectacular results and take note that these are the only such numbers for which this is true.
Taking sums of the powers of the digits of a number leads to interesting results. We can extend this procedure to get a lovely (and not to mention, surprising) technique you can use to have students familiarize themselves with powers of numbers and at the same time try to get to a startling conclusion.
Have them select any number and then find the sum of the cubes of the digits, just as we did above. Of course, for any other number than those above, they will have reached a new number. They should then repeat this process with each succeeding sum until they get into a "loop." A loop can be easily recognized. When they reach a number that they already reached earlier, then they are in a loop. This will become clearer with an example.
Let's begin with the number 352 and find the sum of the cubes of the digits.
The sum of the cubes of the digits of 352 is: 33 + 53 + 23 = 27 + 125 + 8 = 160.
Now we use this sum, 160, and repeat the process:
The sum of the cubes of the digits of 160 is:
13 + 63 + 03 = 1 + 216 + 0 = 217.
Again repeat the process with 217:
The sum of the cubes of the digits of 217 is: 23 + 13 + 73 = 8 + 1 + 343 = 352.
Surprise! This is the same number (352) we started with.
You might think it would have been easier to begin by taking squares. You are in for a surprise. Let's try this with the number 123.
Beginning with 123, the sum of the squares of the digits is: 12 + 22 + 32 = 1 + 4 + 9 = 14.
1. Now using 14, the sum of the squares of the digits is: 12 + 42 = 1 + 16 = 17.
2. Now using 17, the sum of the squares of the digits is: 12 + 72 = 1 + 49 = 50.
3. Now using 50, the sum of the squares of the digits is: 52 + 02 = 25.
4. Now using 25, the sum of the squares of the digits is: 22 + 52 = 4 + 25 = 29.
5. Now using 29, the sum of the squares of the digits is: 22 + 92 = 85.
6. Now using 85, the sum of the squares of the digits is: 82 + 52 = 64 + 25 = 89.
7. Now using 89, the sum of the squares of the digits is: 82 + 92 = 64 + 81 = 145.
8. Now using 145, the sum of the squares of the digits is: 12 + 42 + 52 = 1 + 16 + 25 = 42.
9. Now using 42, the sum of the squares of the digits is: 42 + 22 = 16 + 4 = 20.
10. Now using 20, the sum of the squares of the digits is: 22 + 02 = 4.
11. Now using 4, the sum of the squares of the digits is: 42 = 16.
12. Now using 16, the sum of the squares of the digits is: 12 + 62 = 1 + 36 = 37.
13. Now using 37, the sum of the squares of the digits is: 32 + 72 = 9 + 49 = 58.
14. Now using 58, the sum of the squares of the digits is: 52 + 82 = 25 + 64 = 89.
Notice that the sum, 89, that we just got in step 14 is the same as in step 6, and so a repetition will now begin after step 14. This indicates that we would continue in a loop.
Students may want to experiment with the sums of the powers of the digits of any number and see what interesting results it may lead to. They should be encouraged to look for patterns of loops, and perhaps determine the extent of a loop based on the nature of the original number.
In any case, this intriguing unit can be fun just as it is presented here or it can be a source for further investigation by interested students. We need to bring more of these "spectacular" math wonders to our students!



Leave a comment