THE MATH COLUMN
A Conundrum of Probability in Geometry
By Al Posamentier, Ph.D.
There are times when seemingly-simple issues can be stretched to producing a conundrum that is not easily rectified. One such example is with two concentric circles, where the radius of the smaller circle is one-half the radius of the larger circle as shown in the figure below. The question is: What is the probability that if a point is selected in the larger circle that it is also in the smaller one? The typical (and correct) answer is 1/4. This can easily be shown by letting a smaller circle’s radius, OA, be represented by r, and the large circle’s radius be represented by R, where r = (1/2)R. Then the area small circle is π ((1/2)R)2 = (1/4)πR2, that is, 1/4 of the area of the larger circle, which is πR2.
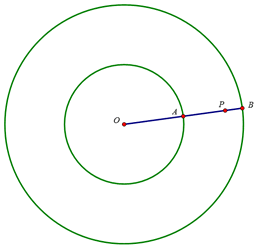Therefore, if a point is selected at random in the larger circle, the probability that it would be in the smaller circle as well is 1/4.
Now here is where the conundrum comes in, as you look at this question differently. The randomly-selected point P must lie on some radius line of the larger circle. Let’s say we will use radius OAB, where A is its midpoint. The probability that a point P on OAB would be on OA (i.e. in the smaller circle) is 1/2, since OA = (1/2)OB. Now, if we were to do this for any other point in the larger circle, we would find the probability of the point being on a radius line and in the smaller circle is 1/2. This, of course, is not correct, although it seems perfectly logical. Where is the error? Here is where you expose the trick, which is actually an attempt to explain a conundrum. The “error” lies in the initial definition of each of two different sample spaces, that is, the set of possible outcomes of an experiment. In the first case, the sample space is the entire area of the larger circle, while in the second case, the sample space is the set of points on a radius such as OAB. Clearly, when a point is selected on OAB, the probability that the point will be on OA is 1/2. These are two entirely different problems even though (to dramatize the issue) they appear to be the same. Conditional probability is an important concept to stress. And what better way to instill this idea than through a demonstration that shows obvious absurdities. Perhaps this conundrum will motivate the you to investigate this further. #
Dr. Al Posamentier is professor emeritus and former dean, CCNY. Now Distinguished Lecturer at NYC College of Technology, Brooklyn, NY.
