THE MATH COLUMN
Caution: Misleading Limits
By Alfred Posamentier, Ph.D.
The concept of a limit is not to be taken lightly. It is a very sophisticated concept that can be easily misinterpreted. Sometimes the issues surrounding the concept are quite subtle. Misunderstanding of limits can lead to some curious situations (or humorous ones, depending on your viewpoint). This can be nicely exhibited with the following two illustrations. Don’t be too upset by the conclusion that you will be led to reach. Remember, this is merely for entertainment. Consider them separately and then notice their connection.
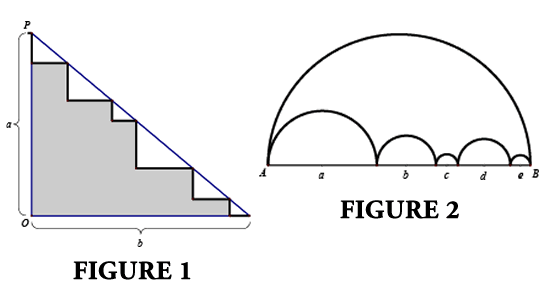
It is simple to see that the sum of the lengths of the bold segments (“stairs”) is equal to a + b, since the sum of the vertical bold lines equals the length OP = a, and the sum of the horizontal bold lines equals OQ = b (see figure 1).
The sum of the bold segments (“stairs”), found by adding all the horizontal and all the vertical segments, is a + b. If the number of stairs increases the sum is still a + b. The dilemma arises when we continue to increase the stairs to a “limit” so that the stairs get smaller and smaller, which then makes the set of stairs appears to be straight line, in this case the hypotenuse PQ of triangle POQ. It would then appear that PQ has length a + b. Yet we know from the Pythagorean Theorem that PQ = a + b √a2 + b2 and not a + b. So what’s wrong? Nothing is wrong! While the set consisting of the stairs does indeed get closer and closer to the straight line segment PQ, it does not therefore, follow that the sum of the bold (horizontal and vertical) lengths approaches the length of PQ, contrary to our intuition. There is no contradiction here, only a failure on the part of our intuition.
Another way to “explain” this dilemma is to argue the following. As the “stairs” get smaller, they increase in number. In the most extreme situation, we have stairs of 0-length in each dimension, used an infinite number of times, which then leads to considering 0 · ∞, which is meaningless! In truth, no matter how small the stairs get, the sum of two adjacent perpendiculars that form one of the small right triangles will never be equal to their hypotenuse. They will just be small right triangles. This may be a bit difficult to see, but that is one of the dangers of working with infinity.
Just as an aside, when considering the set of natural numbers, {1, 2, 3, 4, …}, we would think that it is a larger set than the set of positive even numbers, {2, 4, 6, 8, …}, because all the positive odd numbers are missing from the second set. Yet, since they are infinite sets, they are equal in size! We reason as follows: For every number in the set of natural numbers, there is a “partner” member of the set of positive even numbers; hence they are equal in size. Counterintuitive? Yes, but that is what happens when we consider the concept of infinity.
It appears that infinity is playing games with us. The problem is that when we deal with infinity, we can no longer talk about the equality of sets the way we do when we have finite sets. The same is true with the staircase in our original problem. We can draw the finite steps, yet, we cannot draw the infinite number of steps. Therein lies the problem.
A similar situation arises with the following example. In figure 2, the smaller semicircles extend from one end of the large semicircle’s diameter to the other.
It is easy to show that the sum of the arc-lengths of the smaller semicircles is equal to the arc-length of the larger semicircle. That is, the sum of the smaller semicircles = (Π/2) + (Πb/2) + (Πc/2) + (Πd/2) + (Πe/2) = (Π/2) · (a+b+c+d+e) = (Π/2) · AB,which is the arc length of the larger semicircle. This may not “appear” to be true, but it is! As a matter of fact, as we increase the number of smaller semicircles (where, of course, they get smaller) their sum “appears” to be approaching the length of the segment AB, that is,
(Π / 2) ·AB = AB. Taking this a step further, if we let AB = 1, then we have Π= 2, which we surely know is a mistake!
Again, the set consisting of the semicircles does indeed appear to approach the length of the straight-line segment AB. It does not follow, however, that the sum of the semicircles approaches the length of the limit, in this case AB.
This “apparent limit sum” is absurd, since the shortest distance between points A and B is the length of segment AB, not the semicircle arc AB (which equals the sum of the smaller semicircles). This is an important concept and may be best explained with the help of these motivating illustrations, so that future misinterpretations can be avoided. #
Alfred S. Posamentier, Ph.D., is the Executive Director for Internationalization and Sponsored Programs, Professor Emeritus, Mathematics Education and Former Dean, CCNY-City University of New York.
