THE MATH COLUMN
Motivating Mathematics Instruction Through Counterintuitive Everyday Experiences
By Alfred Posamentier, Ph.D.
In recent years as technology has been advancing at lightning speed to provide ever more attractive and useful features that clearly affect our society, there is a very clear need to improve mathematics instruction in the schools and beyond. In the latter case, although the schools carry the official burden of providing the mathematical background that all students will need to move ahead in this ever-growing technological world, the burden goes beyond the school, specifically to the home environment as well.
First, there is the general misconception that parents should leave the teaching of mathematics to the schools. Although, clearly that is the schools’ responsibility, parents have a clear role to play there as well. This begins with the parents’ attitude towards mathematics. Typically, but not always, parents have a tendency to shirk away from mathematics, and by doing so, indicate to their students, who may be showing parents their day’s school work that their lack of competence in mathematics and perhaps lack of interest as well, guides them to focus more on the student’s work in other subjects, and by doing so downgrade the importance for mathematics. This already gives students a signal that, if mathematics is seen as less important to parents, then it is likely not to be too important for them as well.
The parents influence can be best seen through the following anecdote: a student comes home with two test results: on a test in English a high grade was achieved, while on a test in mathematics a low grade was achieved. A parent who may not have had a good school experience with mathematics instruction – something not uncommon for a large percentage of parents – might respond by lauding the student’s success on the English exam and perhaps placating the student with the poor performance on the mathematics exam. This sends a very detrimental signal. Namely, the parent’s expectation in math is at very low, and so the student can be satisfied performing at that level. As a result, the student is not encouraged to improve performance on the math test and is likely to continue showing a weak mathematics background perceiving its acceptability by parents. In general, this would be a terrible way to guide a youngster; and is especially detrimental in today’s technological world.
Obviously, parents should encourage the student to perform better and never say to the student “I also didn’t do well in mathematics, so don’t worry, as long as you passed the test, it’s OK.” This is just one important aspect that parents need to consider as they arear their students to be successful in school, and especially in mathematics. As a complete flip from this negative behavior, parents would do well to begin to fortify themselves with simple mathematics concepts and ideas that are not necessarily presented as part of the school curriculum. Time spent preparing themselves with these new ideas can be internally rewarding, and externally it would be enriching their children’s mathematical experience, which should carry over as motivation for more actively learning the subject in school.
There are many resources for parents to build up this arsenal of ideas that will not only entertain the parents as they familiarize themselves with these new concepts, but they will also find it enjoyable to interact with their child on a mathematical topic that will engender amazement and demonstrate the power and beauty of mathematics. Before we present some of these ideas to merely whet the reader’s appetite, we need to address the role of the teacher in an analogous approach.
With the advent of teaching standards and a regular regiment of standardized testing, mathematics teachers today are strongly guided to follow these guidelines and are subjected to related professional assessments. As a result, teachers rarely deviate from the prescribed curriculum, and moreover, they emphasize preparation for the various examinations which students will encounter along their instructional path. This obsessive instruction often time takes the “fun” out of teaching and learning mathematics. Just as we are advocating that parents familiarize themselves with some off-the-beaten-path mathematical concepts and ideas that can be highly motivating, teachers should take the time each week to deviate from the prescribed curriculum and expose students to these mathematical wonders. While presenting these typically not-well-known ideas, teachers have a tendency to generate special enthusiasm in their presentation, which further serves to motivate the students to the point where the time spent on this deviation is an investment whose dividends are seen as a more receptive learner for the required curriculum.
One of the most neglected aspect of teaching mathematics over the past several decades has been the teacher’s interest in seeking unusual aspects of mathematics that can be used to motivate the subject so that the learners will be eager to learn this required subject, rather than to feel obligated to learn it as part of this school experience. In recent years, this neglect has even gotten more obvious, since the evaluation of teacher performance has become paramount in most countries. School performance is typically measured by how well students perform in the key subjects, such as mathematics. With the increase of technology in the instructional program, regular testing of students has become more prevalent and also more statistically ripe for comparison purposes. All too often, teachers are observed to be “teaching to the test” as they feel that their evaluation and teaching performance will be based on the test results of their students. All of this mitigates against deviating from the tested materials to other aspects of mathematics that are not part of the curriculum. At the same time, it is clear that motivated students are more receptive learners. It is unfortunate that throughout most teacher training programs, potential teachers are not exposed to many extracurricular topics that can be used to interest students. Some of these unusual topics are often surprising or counterintuitive. Not only are they are in and of themselves attractive, but they can also be useful for better understanding everyday life experiences. Presentation of these topics is then complicated by teachers not wanting to deviate from the prescribed curriculum for fear of using time that could otherwise be more directed at the required curriculum. So, what are some of these unusual topics? Let us consider a few of these now; and be aware that parents as well as teachers can use them productively to make mathematics come alive. As we explore some of these examples, take note how their counterintuitive nature in and of itself is motivating since it demonstrates how learning mathematics helps us navigate through our lives.
We begin with a question that most have never thought to ask themselves. When we walk over manhole covers in the street, we take for granted that they are always circular. The question is, why are they always circular in shape? Well, the reason is very simple: As you can see in figure 1, the circular shape cover can never fall into the hole, as would be the case with a square shape cover.
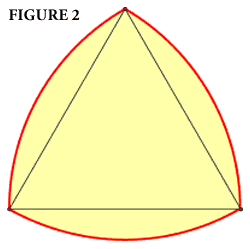
Here is where the topic gets enlarged and should be of even greater interest to students. It is then natural to ask if there is any other shape that can be used to cover a manhole and that will also not be able to fall into the hole? The answer was provided by the German engineer Franz Reuleaux (1829 – 1905), who developed a rather odd-looking shape that is now called a Reuleaux triangle, which we show in figure 2. This is created by beginning with an equilateral triangle and drawing a circular arc on each side with the circle’s center at the opposite vertex.
One might wonder how Franz Reuleaux ever thought of this triangle. It turns out that he was in search of a button that was not round, but still could fit through a button hole equally well from any orientation. His “triangle” solved the problem, as seen in figure 3.
Figure 4 shows one such manhole cover in the shape of a Reuleaux triangle.
This becomes particularly significant when fire hydrants are designed so that only special tools can turn them on. Often, a pentagonal valve screw is used since a common wrench – which requires two parallel sides – cannot be used, as would be the case with a hexagonal or a square valve screw, each of which has a pair of parallel opposite sides.
A Reuleaux triangle type valve screw, which has the same properties as a circle, but can only be turned with a wrench of exactly the same shape. One such example of a fire hydrant is shown in figure 5.
An ambitious parent or a teacher who would like to tie this discussion into the curriculum, might want to pursue the connection between the Reuleaux triangle and the circle. A curious property of the Reuleaux triangle is that the ratio of its perimeter to its breadth, which is ((1/2 • 2πr) / r) = π, is the same as that ratio for a circle, (2πr/2r) = π.
The comparison of the areas of these two shapes is quite another thing, and could be useful when deciding what shape to make a manhole cover. The area of the Reuleaux triangle can be obtained by adding the three circle sectors that overlap the equilateral triangle and then deducting the pieces that overlap, which is twice the area of the equilateral triangle.The total area of the three overlapping circle sectors, where each is 1/6 of the area of the circle, is equal to 3 (1/6)(πr2). From this we need to subtract twice the area of the equilateral triangle, which is (r2 √3) / 4. Therefore, the area of the Reuleaux triangle is equal to
3(1/6)(πr2)-2((r2 √3)/4)=((r2/2)(π - √3)) ≈ r2((3.1416 – 1.732)/2)= 0.7048 • r2, while the area of a circle with diameter of length r is equal to (π(r/2)2) = (πr2)/4 = 0.7854 • r2.
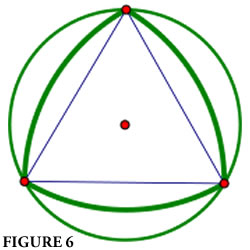
Therefore, the area of the Reuleaux triangle is less than the area of the circle, which we can also see rather clearly in figure 6. This is consistent with our understanding of regular polygons, where the circle has the largest area for a given diameter.
Therefore, from a practical standpoint, to design a manhole cover of a given breadth, and one that would not be able to fall into the hole, the Reuleaux triangle shape would be the economic choice as it would require less metal construct. Here is an interesting application of some genuine mathematics applied to a piece of our environment that we seem to take for granted.
Percentage problems have long been a nemesis for many people, and unfortunately tediously taught in the schools. Problems get particularly unpleasant when multiple percentages need to be calculated for the same base. Suppose a store is offering a 20% discount on top of an already discounted price of 10%. Intuitively, many people will assume that is the equivalent of a 30% discount. This, of course, is not true!
Perhaps an easy way to explain this issue would be to assume the cost of the item to be $100, calculate the 10% discount yielding a $90 price, and an additional 20% of the $90 price (or $18) will bring the price down to $72, indicating a 28% discount; not a 30% discount. Some people would consider this to be counterintuitive. They would also consider it counterintuitive if a store offered a 10% discount one day and on the next day raised their prices by 10% that they would not come back to the original price, but in fact would represent a discount of 1%.
A truly counterintuitive example in mathematics is to ask which of the American 48 continental states is closest to the African continent? A common reaction to this question is the state of Florida. However, when looking at the globe of the earth, we find that the distance from the state of Maine – all the way at the northeastern section of the United States – is closest to the African continent. This amazes many people and could serve nicely as an introduction of the geometry on a sphere, which could also explain why, the path of the airplane traveling from New York to Vienna often time flies over a portion of Greenland, which is truly unexpected. An entertaining question about the globe of the earth would be to determine where one could start a walk, which would start with 1 mile South then 1 mile East then 1 mile North and end up back at the starting point?
There are many other counterintuitive examples in mathematics, each of which would not only be entertaining by their stunningly unexpected results, but also could be used to lead into topics in the standard curriculum. For example, when introducing the concept of probability, it would be motivating to begin with a shocking result, such as the following: with 366 birthdates available, in a group of about 55 people, the probability of two people having the same birthdate (not the year) is practically 100%. This is easily calculable. From a group of 55 students the probability that one student matches his own birthdate would be 1, and can be written as 365/365.
The probability that another student’s birthdate does not match the first student’s is (365 – 1)/365 = 364/365.
The probability that a third student’s birthday does not match the first and second student’s birthday is (365 – 2)/365 = 363/365.
The probability of all 55 students not having the same birth date is the product of these probabilities: p = (365/365)g((365-1)/365)g((365-2)/365)gL g((365-54)/365).
Since the probability (q) that two students in the group have the same birth date, and the probability (p) that two students in the group do not have the same birth date is a certainty, the sum of those probabilities must be 1. Thus, p + q = 1. In this case, q = 1 - (365/365)g((365-1)/365)g((365-2)/365)gL g((365-53)/365)g((365-54)/365) ≈ .9862623 ≈ .99. In other words, the probability that there will be a birthdate match in a randomly selected group of 55 people is about 99%. Quite unexpected!
There a lot of other questions we can ask, and which have results that are against what our intuition would lead us to. For example, one would think that the 13th of the month is equally likely to appear on any of the seven days of the week. However, mathematically we can show that it appears more frequently on Friday than any other day the week.
In finance, mathematics also plays an important role. For example, if one wants to determine how long it will take to double money in a bank account that is compounded daily, all one needs to do is to divide 72 by the interest rate and you get a very close approximation to the right answer. For example, if one is getting 4% interest compounded daily, it will take (72/4) = 18 years to the double the money.
Here’s an entertaining dilemma. Suppose we let S = 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + . . .
By pairing the numbers of the series as follows:
= (1 – 1) + (1 – 1) + (1 – 1) + (1 – 1) + . . . = 0 + 0 + 0 + 0 + . . . = 0
However, were we to group this differently, we would get:
S = 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + . . . = 1 – (1 – 1) – (1 – 1) – (1 – 1) – . . . = 1 – 0 – 0 – 0 – . = 1.
How can S = 1, and also have S = 0? This “upsetting” result can nicely lead into a discussion of infinity, which offers many counterintuitive illustrations, such as why is the set of counting numbers, or natural numbers, equal to the set of even numbers, when the first set includes all the odd numbers, omitted from the second set.
Then there are questions that open up some useful investigations, such as why does a number which is divisible by three (or 9) have a digit sum divisible by three (or 9)?
Parents and teachers can also have fun with some mathematical curiosities. One such is to select any three-digit number where the units and the hundreds digit are not the same. Subtract this numbers and its reversal. Then take this difference and once again reverse the digits and then add these last two numbers. Regardless of which number you began with, you will always get the number 1,089.
Such curiosities tend to amaze students and can be presented by parents and teachers. In the latter case, it would be wise to use them to introduce topics in the curriculum. However, overarchingly, this approach to introducing mathematical curiosities should go a long way in changing many students’ perception of mathematics to the point where – if it is done often enough would promote very favorable learning conditions. #
Alfred S. Posamentier, Ph.D., is the Executive Director for Internationalization and Sponsored Programs, Professor Emeritus, Mathematics Education and Former Dean, CCNY-City University of New York.
