Although the amazing geometric phenomenon we are about to present is attributed to Napoleon Bonaparte (1769-1821), some critics assert that the theorem was actually discovered by one of the many mathematicians with whom Napoleon liked to interact. Yes, Napoleon took pride in his ability in mathematics. Perhaps this aspect of his values is a good model for us all to follow.
Simply stated, we begin our exploration of this geometric novelty with a scalene triangle — that is, one that has all sides of different lengths. We then draw an equilateral triangle on each of the sides of this triangle. Next, we will draw line segments joining the remote vertex of each equilateral triangle with the opposite vertex of the original triangle. (See Figure 1.)
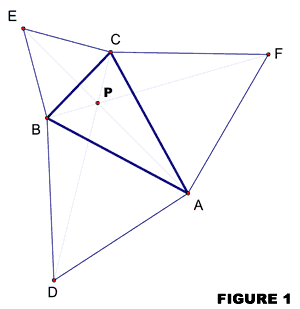
There are two important properties that evolve here — and not to be taken for granted — namely, the three line segments we just drew are concurrent (that is, they contain a common point) and they are of equal length. Remember, this is true for a randomly selected triangle, which implies it is true for all triangles — that’s the amazing part of this relationship.
Furthermore, of all the infinitely many points in the original scalene triangle, the point of concurrency is the point from which then sum of the distances to the three vertices of the original triangle is the shortest.[1] That is, in figure C, from the point P, the sum of the distances to the vertices A, B and C (that is, PA + PB + PC) is a minimum. Also, the angles formed by the vertices of the original triangle at point P are equal. In figure 1, ∠APB = ∠APC = ∠BPC ( = 120°). This point, P, is called the Fermat point, named after the French mathematician, Pierre de Fermat (1607-1665).
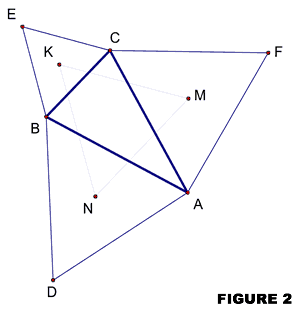
Now to Napoleon’s triangle: When we join the center points of the three equilateral triangles (i.e. the point of intersection of the medians, angle bisectors, and altitudes), we obtain another equilateral triangle — called the outer Napoleon triangle, in figure 2 it is ΔKMN. Remember this is for any triangle ABC.
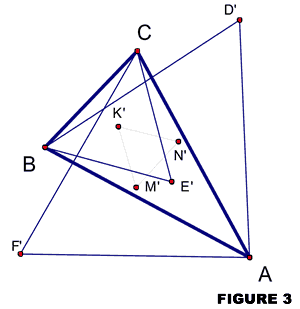
Had the three equilateral triangles — on each side of the scalene triangle – been drawn overlapping the original scalene triangle, then the center points of the three equilateral triangles would still determine an equilateral triangle. This is depicted in figure 3 as ΔK’M’N’. It is called the inner Napoleon triangle.
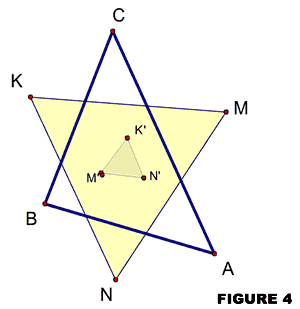
Now something comes up that may a bit hard to picture. Let’s consider the two Napoleon triangles in the same diagram, which can be more easily seen if we omit the generating side-equilateral triangles, as shown in figure 4.
Consider the areas of the three triangles in the figure 4. The difference of the areas of the two Napoleon triangles (the inner and the outer) is equal to the area of the original scalene triangle. Thus,
Area ΔKMN – Area ΔK’M’N’ = Area ΔABC.
Again, we remind you, that what makes this so spectacular is that it is true for any shape of an original triangle, which we tried to dramatize by using a scalene triangle that does not have any special properties.
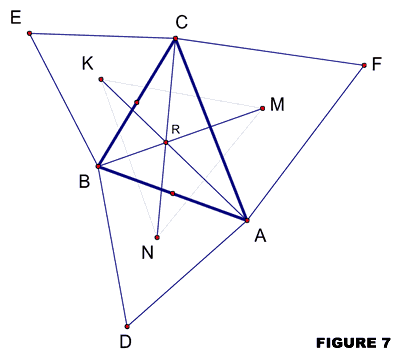
When we view the original triangle and the Napoleon triangles, they share the same centroid — i.e. the point of intersection of the medians, which is also center of gravity of the triangle. (See figure 5, where we show only the outer Napoleon triangle for clarity, but it is also true for the inner Napoleon triangle.)
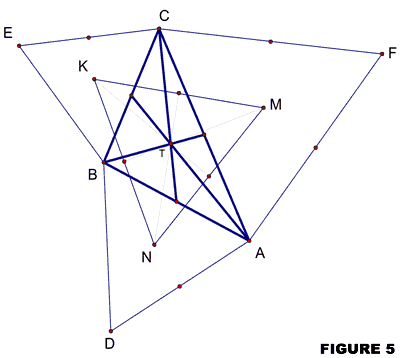
There are more surprising relationships that can be found on this Napoleon triangle. These were derived long after Napoleon (as he claimed) discovered the very basics of the equilateral triangle that evolved from the random triangle. Take, for example, the lines joining each vertex of the outer Napoleon triangle[2] to the vertex of the corresponding equilateral triangle drawn on the side of the original scalene triangle. First we can show that these three lines are concurrent. That is, DN, EK, and FM meet at the common point O. Second, this point of concurrency, O, is the center of the circumscribed circle of the original triangle. (See Figure 6).
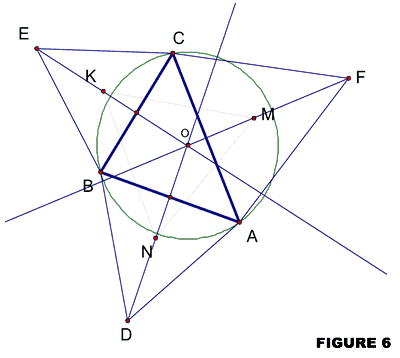
Believe it or not, there is even another concurrency in this figure. If we consider the lines joining a vertex of the Napoleon triangle with the remote vertex of the original triangle, we again get a concurrency of the three lines. In figure 7, AK, BM, and CN are just such lines and are concurrent.
You may, by this point, get the feeling that just about anytime you have three “related” lines in a triangle, they must be concurrent. Well, to appreciate the concurrencies we have just presented, suffice it to say, concurrencies are not common. They may be considered exceptional when they occur. So that ought to make you really appreciate them! Read more about this and other geometric phenomena in the newly published book: The Secrets of Triangles: A Mathematical Journey By Alfred S. Posamentier and Ingmar Lehmann (Prometheus Books, 2012).
-------------------
[1] This is based on a triangle that has no angle greater than 120°. If the triangle has and angle greater than 120°, then the desired point is the vertex of the obtuse angle.
[2] We shall use the outer one, just for clarity, but it would hold true for the inner one as well.
Simply stated, we begin our exploration of this geometric novelty with a scalene triangle — that is, one that has all sides of different lengths. We then draw an equilateral triangle on each of the sides of this triangle. Next, we will draw line segments joining the remote vertex of each equilateral triangle with the opposite vertex of the original triangle. (See Figure 1.)

There are two important properties that evolve here — and not to be taken for granted — namely, the three line segments we just drew are concurrent (that is, they contain a common point) and they are of equal length. Remember, this is true for a randomly selected triangle, which implies it is true for all triangles — that’s the amazing part of this relationship.
Furthermore, of all the infinitely many points in the original scalene triangle, the point of concurrency is the point from which then sum of the distances to the three vertices of the original triangle is the shortest.[1] That is, in figure C, from the point P, the sum of the distances to the vertices A, B and C (that is, PA + PB + PC) is a minimum. Also, the angles formed by the vertices of the original triangle at point P are equal. In figure 1, ∠APB = ∠APC = ∠BPC ( = 120°). This point, P, is called the Fermat point, named after the French mathematician, Pierre de Fermat (1607-1665).
Now to Napoleon’s triangle: When we join the center points of the three equilateral triangles (i.e. the point of intersection of the medians, angle bisectors, and altitudes), we obtain another equilateral triangle — called the outer Napoleon triangle, in figure 2 it is ΔKMN. Remember this is for any triangle ABC.

Had the three equilateral triangles — on each side of the scalene triangle – been drawn overlapping the original scalene triangle, then the center points of the three equilateral triangles would still determine an equilateral triangle. This is depicted in figure 3 as ΔK’M’N’. It is called the inner Napoleon triangle.

Now something comes up that may a bit hard to picture. Let’s consider the two Napoleon triangles in the same diagram, which can be more easily seen if we omit the generating side-equilateral triangles, as shown in figure 4.
Consider the areas of the three triangles in the figure 4. The difference of the areas of the two Napoleon triangles (the inner and the outer) is equal to the area of the original scalene triangle. Thus,
Area ΔKMN – Area ΔK’M’N’ = Area ΔABC.
Again, we remind you, that what makes this so spectacular is that it is true for any shape of an original triangle, which we tried to dramatize by using a scalene triangle that does not have any special properties.

When we view the original triangle and the Napoleon triangles, they share the same centroid — i.e. the point of intersection of the medians, which is also center of gravity of the triangle. (See figure 5, where we show only the outer Napoleon triangle for clarity, but it is also true for the inner Napoleon triangle.)

There are more surprising relationships that can be found on this Napoleon triangle. These were derived long after Napoleon (as he claimed) discovered the very basics of the equilateral triangle that evolved from the random triangle. Take, for example, the lines joining each vertex of the outer Napoleon triangle[2] to the vertex of the corresponding equilateral triangle drawn on the side of the original scalene triangle. First we can show that these three lines are concurrent. That is, DN, EK, and FM meet at the common point O. Second, this point of concurrency, O, is the center of the circumscribed circle of the original triangle. (See Figure 6).

Believe it or not, there is even another concurrency in this figure. If we consider the lines joining a vertex of the Napoleon triangle with the remote vertex of the original triangle, we again get a concurrency of the three lines. In figure 7, AK, BM, and CN are just such lines and are concurrent.

You may, by this point, get the feeling that just about anytime you have three “related” lines in a triangle, they must be concurrent. Well, to appreciate the concurrencies we have just presented, suffice it to say, concurrencies are not common. They may be considered exceptional when they occur. So that ought to make you really appreciate them! Read more about this and other geometric phenomena in the newly published book: The Secrets of Triangles: A Mathematical Journey By Alfred S. Posamentier and Ingmar Lehmann (Prometheus Books, 2012).
-------------------
[1] This is based on a triangle that has no angle greater than 120°. If the triangle has and angle greater than 120°, then the desired point is the vertex of the obtuse angle.
[2] We shall use the outer one, just for clarity, but it would hold true for the inner one as well.


