There are often unusual phenomena in mathematics that pique one's interest. This is not a trick. Yet mathematics does provide curiosities that appear to be magic. This is one that has baffled mathematicians for many years and still no one knows why it happens. Try it, you'll like it -- or least the students will!
Begin by asking your students to follow two rules as they work with any arbitrarily selected number.
If the number is odd then multiply by 3 and add 1.
If the number is even then divide by 2.
Regardless of the number they select, they will always end up with 1.
Let's try it for the arbitrarily selected number 12
12 is even, therefore, divide by 2 to get 6.
6 is also even so we again divide by 2 to get 3.
3 is odd, therefore, multiply by 3 and add 1 to get 3 • 3+1=10
10 is even, so we simply divide by 2 to get: 5
5 is odd, so we multiply by 3 and add 1 to get 16.
16 is even so we divide by 2 to get 8.
8 is even so we divide by 2 to get 4.
4 is even so we divide by 2 to get 2.
2 is even so we divide by 2 to get 1.
No matter which number we begin with (here we started with 12) we will eventually get to 1.
This is truly remarkable! Try it for some other numbers to convince yourself that it really does work. Had we started with 17 as our arbitrarily selected number we would have required 13 steps to reach 1. Starting with 43 will require 27 steps. You ought to have your students try this little scheme for any number they choose and see if they can get the number 1.
Does this really work for all numbers? This is a question that has concerned mathematicians since the 1930s, and to date no answer has been found, despite monetary rewards having been offered for a proof of this conjecture. Most recently (using computers) this problem, known in the literature as the "3n + 1 Problem," has been shown to be true for the numbers up to 1018 - 1.
For those who have been turned on by this curious number property, we offer you a schematic that shows the sequence of start numbers from 1 to 20.
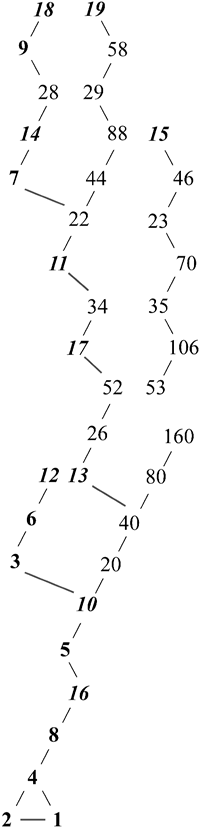
Notice that you will always end up with the final loop of 4-2-1. That is, when you reach 4 you will always get to the 1, and then, were you to try to continue after having arrived at the 1, you will always get back to the 1, since, by applying the rule [3 • 1 + 1 = 4] and you continue in the loop: 4-2-1.
Does this really work for all numbers? This amazing little loop-generating scheme was first discovered in 1932 by the German mathematician Lothar Collatz (1910-1990), who then published it in 1937. Credit is also given to the American mathematician Stanislaus Marcin Ulam (1909-1984), who worked on the Manhattan Project during World War II, and to the German mathematician Helmut Hasse (1898-1979). Therefore, the scheme (or algorithm) can be found under various names.
A proof that this holds for all numbers has not yet been found. The famous Canadian mathematician H. S. M. Coxeter (1907-2003) offered a prize of $50 to anyone who could come up with such a proof, and $100 for anyone who could find a number for which this doesn't work. Later, the Hungarian mathematician Paul Erdös (1913-1996) raised the prize money to $500. Still, with all these and many further incentives, no one has yet found a proof. This seemingly "true" algorithm then must remain a conjecture until it is proved true for all cases.
Most recently (with aid of computers), the "3n + 1 Problem" has been shown to be true for the numbers up to 18 • 258 ≈ 5.188146770 • 1018 (June 1, 2008). That means, for more than 5 Quintillion [in Europe: trillion] it is proved.
We don't want to discourage inspection of this curiosity, but we want to warn you not to get frustrated if you cannot prove that it is true in all cases, for the best mathematical minds have not been able to do this for the better part of a century! Explain to your students that not all that we know or believe to be true in mathematics has been proved. There are still many "facts" that we must accept without proof, but we do so knowing that there may be a time when they will either be proved true for all cases, or someone will find a case for which a statement is not true, even after we have "accepted it."
With this unusual demonstration you should begin the year 2011
with a favorable view of mathematics.

